Jo, Eunkyung (Ara)

Lab Manager, M.A. in Psychology

1 minute read


이 페이지는 MarinStatsLectures-R Programming & Statistics의 강의를 바탕으로 작성되었다.

1. 데이터 가져오기

데이터는 MarinStatsLectures에 공개되어 있는 ‘LungCap Dataset’을 사용했다.


1-1. 라이브러리 열기

library("readxl")



1-2. 데이터 찾기

데이터 프레임의 이름을 설정해주고 다운로드한 파일을 찾아준다.

LungCapData <- read_excel(file.choose())


1-3. 데이터 확인

names(데이터프레임 이름)를 입력해서 데이터를 확인해준다. 나는 데이터프레임을 ‘LungCapdata’로 설정했으므로 괄호안에 ‘LungCapData’를 넣어주면 된다.

> names(LungCap)
[1] "LungCap"   "Age"       "Height"    "Smoke"     "Gender"    "Caesarean"

여기서 이번 분석을 위한 변인은 다음과 같다.

  • 독립변인: Smoke
  • 종속변인: LungCap

확인을 마쳤으면 attach(데이터프레임 이름)을 실행해서 변수명들을 바로 사용할 수 있게 해준다.

attach(LungCapData)



1-4. 변수 속성 확인

t-test를 진행하기 위해 기본적으로 독립변인과 종속변인의 속성이 적합한지 확인하기 위해 class()를 사용해준다. 

> class(LungCap)
[1] "numeric"
> class(Smoke)
[1] "character"



1-5. 변수 속성 바꾸기

t-test를 수행하기 위해서는 LungCap은 numeric, Smoke(흡연여부)는 factor로 출력되어야 하는데, Smoke가 character로 되어 있다. 이걸 factor로 바꿔주자.

> Smoke2 <-Smoke    #변수를 복제해준다.
> class(Smoke2)
[1] "character"
> Smoke2 <-as.factor(Smoke2)    #Smoke2의 변수 속성을 factor로 전환해준다.


이렇게 생성된 Smoke2의 속성을 다시 class(Smoke2)를 입력해서 확인해준다.
levels(Smoke2)를 입력하면 아래와 같이 변인이 어떤 값으로 이루어져 있는지 확인할 수 있다.

> class(Smoke2)
[1] "factor"
> levels(Smoke2)
[1] "no"  "yes"




2. box plot 그리기

boxplot(종속변수 ~ 독립변수)를 이용해서 boxplot을 먼저 그려본다.

boxplot(LungCap ~ Smoke2)


그러면 아래와 같이 boxplot이 출력된다.




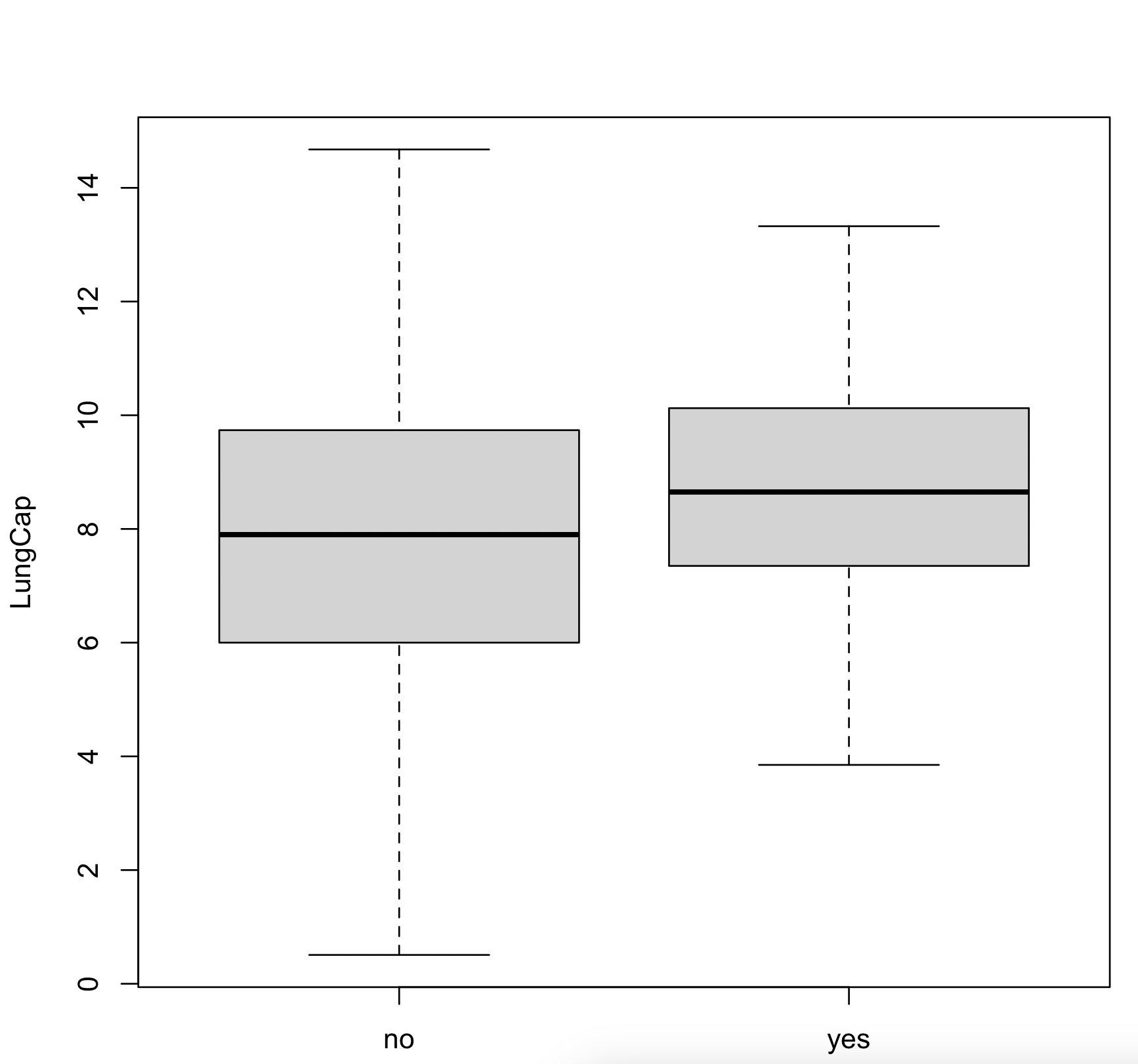
3. 독립 t-test 분석하기

귀무가설은 다음과 같다.
Ho: mean lung cap of smokers = of non-smokers (흡연자와 비흡연자의 페활량에는 차이가 없다)
분석을 위해 코드는 아래와 같이 입력해준다.

t.test(LungCap ~ Smoke2, mu=0, alt="two.sided", conf=0.95, var.eq=F, paired=f)



코드를 하나씩 뜯어보면 아래와 같다.
흔히 많이 쓰이는 방법으로 독립표본 t-test를 진행하는 경우에는 간단하게 t.test(종속변인 ~ 독립변인)이라고만 쳐도 동일한 결과가 나온다.

t.test(종속변수 ~ 독립변수, 
        mu=0, #귀무가설은, 흡연자와 비흡연자간의 종속변인 평균에 차이가 없다. 디폴트값.
        alt="two.sided", #양측검정. 디폴트값.
        conf=0.95, #신뢰수준. 디폴트값.
        var.eq=F, #분산의 동질성. F는 같지 않음. 디폴트값. 
        paired=F #대응표본 t-test인지 확인. f는 독립표본. 디폴트값.
        )



그렇게하면 나오는 결과.

> t.test(LungCap ~ Smoke2)

	Welch Two Sample t-test

data:  LungCap by Smoke2
t = -3.6498, df = 117.72, p-value = 0.0003927
alternative hypothesis: true difference in means between group no and group yes is not equal to 0
95 percent confidence interval:
 -1.3501778 -0.4003548
sample estimates:
 mean in group no mean in group yes 
         7.770188          8.645455

You may also enjoy